In Part 1, I wrote:

When done accurately and before any clever processing, the number of cashflows produced can easily run into the millions, and for a large pension plan, into the billions. (When I have time, I plan to explain why, and talk about some of the clever processing that can be done).

This situation is one that obviously calls for parallel or distributed processing, with the work shared out between many machines.

In this post, I explain why so many cashflows are produced when calculations are done accurately.

Example UK defined benefit pension plan

Let's consider an example UK defined benefit pension plan, with roughly equal numbers of active, deferred pensioners and pensioners. (Individual pension plans will differ significantly from this, but this simplistic mix is not far from reality for several large pension plans). Let's assume that the pensioners are split in the ratio 20:14 between pensioners and partners (widows/widowers) - again simplistic but not unreasonable/atypical.

For round numbers, let's assume 33% active membership, 33% deferred pensioners (dps), 20% pensioners and 14% partners. For illustration, let's also assume that the average age of the actives is 37, those of the dps is 48, the pensioners 69 and the partners 73.  For simplicity, we will take members of these ages as representative model points for each class, and later on we will apply the 33%/33%/20%/14% weightings to determine the expected total number of cashflows. (The true calculation adds up the cashflows from each member in each membership category, but for ease of demonstration the approach taken in this article will suffice to illustrate the point. We will also see that the average age assumed for categories other than active members is of relatively little importance: it is the actives who produce the vast bulk of the cashflows). 

We will also assume for simplicity that pension plan members have a partner who is 3 years younger than them. (Again, in practice this will vary, but this is not a material factor in determining the scale of the number of cashflows required). 

Let's also assume that the pension plan's normal retirement age is 65, and that on average, members have two different slices of benefits (i.e. their benefits are split into two parts, each of which - due to changes in plan rules or legislation - has different pension increases or other behaviour).  Let's also assume that one of those slices includes some GMPs (Guaranteed Minimum Pensions), and that the terminal age of the mortality tables used is 120, i.e. no member or their partner is assumed to live beyond age 120).

How many cashflows should we expect from each of our representative members?

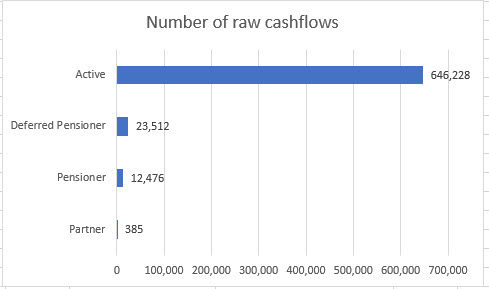
385 cashflows arising from the partner (widow/widower) member

The simplest case is that of the partner.  Here for each benefit slice, payments will continue to be made from the current age, 73, to the terminal age, 120.  So for the slice without GMPs there should be 120 - 73 = 47 years of payments. In reality there would be 47 * 12 = 564 monthly payments,  probably 570 payments including the final six during age 120 (death occurs after reaching that age and to first order is assumed to occur half way through the year).  But it is common in pension plan projections to use annual payments.   (If we don't then the number of cashflows is further increased beyond the already large numbers shown in this post). 

To allow for discounting and pension increases during the year, the 12 monthly payments can be approximated very well by two payments, one at the beginning and one at the end of each projection year.

That leads to 47 * 2 + 1 = 95 cashflow payments (including the very last one, paid on reaching age 120.  

That is for the benefit slice without GMPs.  For the slice including GMPs, there will be 3 times as many payments (excess over GMP, Pre 1988 GMP, and Post 1988 GMP).  (Technically speaking, for a female partner, there would have been no pre 1988 GMP, but we will ignore this for the purposes of this post, and besides the recent ruling on GMP equalisation may change this retrospectively!).

So we have 95 * (1 + 3) = 385 cashflows for the partner.

12k cashflows arising from the pensioner member

This is slightly more complicated, because as well as the cashflows being paid to the pensioner, we need to allow for cashflows being paid each year (and subsequent years) to a new partner member of the plan on death of the pensioner during each projection year. (For simplicity I am ignoring here and below the very small number of cashflows arising from payment of a lump sum to a deferred pensioner or active on retirement, and also on the death of a pensioner under a pensions guarantee period, normally  of up to 5 years).

Given that the age of the pensioner is 69, there will be (following the approach shown above for the partner), there will be 120 - 69 = 51 years of payments, leading to 51 * 2 + 1 = 103 payments allowing for a final payment on reaching age 120. That would be for the benefits slice with no GMP.  After allowing for the slice with a GMP, in total there will be 103 * (1 + 3) = 412 cashflows paid to the pensioner.

But for each projection year (from age 69 to 120, including the year following on from age 120 to 121), there is a non zero probability that the pensioner will die during the year, so 120 - 69 + 1 = 52 occasions on which partner payments start being paid. (Of course these partners are normally assumed to be all the same person and that is one of the bits of processing that can be done to cut down the number of cashflows, but for the moment we are talking about the number of raw cashflows that need to be produced).  Each of these will have two benefit slices, one of which includes GMP. 

Analogously to the approach shown above for the partner aged 73, the partner arising on death of the pensioner during the year of age 69 to 70 will be aged 69 - 3 = 66 (66.5 in practice but I am ignoring  the half year for simplicity in this post) and will lead to 120 - 66 = 54 years of payments, leading to 54 *2 + 1= 109 cashflows. The partner arising on death during the year of age 70 to 71 will lead to 120 - 67 + 1 = 53 years of payments, leading to 53 * 2 + 1 = 107 cashflows, etc, right up to the partner arising on death during the year of age 120 to 121 leading to 120 - 117 = 3 years of payments with 3 * 2 + 1 = 7 cashflows.  

This is a total of 109 + 107 + 105 + .... + 7 = 3,016 cashflows. 

Allowing for the two slices, one of which has GMPs, this means that the total number of cashflows paid to partners is 3016 * (1 + 3) = 12,064.

Overall, the number of cashflows arising from the pensioner member is 412 + 12064 = 12,476.

23k cashflows arising from the deferred pensioner member

This is slightly more complicated still, because as well as the cashflows that will be paid on (and following) retirement to the deferred pensioner (and to a partner on death after retirement), we need to allow for cashflows being paid each year (and subsequent years) to a new partner member of the plan on death of the deferred pensioner before retirement. (We could also allow for potential early retirement of the deferred pensioner on ill health, but unlike for active members, where the benefits on ill health retirement can be more generous and hence more financially significant, this complication has been commonly ignored - because leading to a slight overstatement of the liability, hence a slight element of prudence - in the valuation of deferred pensioners.  So I ignore this here for simplicity).

Analogously to the approach taken above for the pensioner member, but applied to a pensioner aged 65 (the normal retirement age), that pensioner will lead to 

(120 - 65) * 2 + 1 = 111 payments for the slice without GMP, and a total of 111 * (1 + 3) = 444 cashflows paid to the pensioner. 

Plus, on death of the pensioner after retirement, starting with 120 - 62 = 58 years of payment or 58 * 2 + 1 = 117 cashflows: 

117 + 115 + 113 + ... + 7 = 3,472 cashflows paid to the partner for the slice with no GMPs, and a total of 3472 * (1 + 3) = 13,888 cashflows paid to a partner arising from death after retirement.

Analogously, for death  before retirement (during the period of years of age 48-49, 49-50 up to 64-65), starting with (120 - 45) * 2 + 1 = 151, and ending with (120 - 61) * 2 + 1 = 119:

151 + 149 + .... + 119 = 2,295 cashflows paid to the partner for the slice with no GMPs, and a total of 2295 * 4 = 9,180 cashflows paid to a partner arising from death before retirement.

Overall the number of cashflows arising from the deferred pensioner member is 444 + 13,888 + 9,180 = 23,512.

Over half a million cashflows arising from the active member!

This is considerably more complicated because, before normal retirement age 65, we also need to allow for leaving service, ill health retirement and death in service.

Exactly analogously to the approach taken for the deferred pensioner member, there will be a total of 444 + 13,888 = 14,332 cashflows arising from normal retirement at age 65.

But in addition, there are huge numbers of cashflows arising during each of the years of age 37 to 38, 38 to 39, ..., 64 to 65  from possible:

• leaving service: each deferred pensioner created will generate several thousand cashflow records (some 23,000 on leaving service at age 48 as you can see from the dp case above, more at younger ages)
• retirement on ill health: each ill health pensioner created will generate fewer but still several thousand cashflow records (in each case more than the 14,332 generated at age 65 on normal retirement, because the member is younger)  
• death in service: each partner created will generate over a hundred cashflow records

The calculations are clearly very tedious to do by hand (or with Excel), so I used software (InQA Limited's Pensions Concerto valuation and cashflow projection tool).

Overall the number of cashflows arising from the active member (this time including the small number of extra cashflows arising from lump sums on retirement, and payment of pension guarantees on death) was over half a million at 646,228. 

How many raw cashflows need to be produced for a medium plan? for a very large plan?

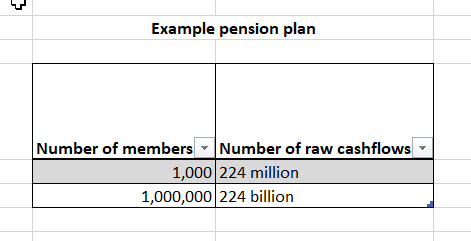
For a thousand member pension plan, with the membership weighted in the stated proportions (33% actives, 33% deferred pensioners, 20% pensioners and 14 % partners), and using the above members as broadly representative, the number of cashflows produced is:

330 * 646,228 + 330 * 23,512 + 200 * 12,476 + 140 * 385 = 223,563,300 or 224 million.

As mentioned before, the actives clearly produce the vast bulk of the cashflows (95% in this case), so it matters relatively little what average age is assumed for the other membership categories.

For a million member plan, the number of cashflows produced would be 224 billion. 

This is not all.  For a continuing pension plan, it is usually necessary to calculate the contribution rate required to fund future accrual, both during a short term period (e.g. the next year), and during the future working lifetime of current active members. In order to do this, three sets of cashflows need to be calculated for active members: the above one (for past service, based on benefits accrued at the valuation date), the benefits that will be produced allowing for accrual during the short term period (e.g. the next year), and the benefits that will be produced allowing for accrual during the future working lifetime.

These are the raw cashflows.  Can we do anything to speed up the processing?

The above are the cashflows that need to be produced at some point during the calculations, in order to do things accurately before any smart processing, and if you want to be able to value each member individually. This can be done with distributed processing and big data treatment/storage.

Of course instead of performing the calculations on individual members, you could perform the calculations on grouped data. If you do this, it is important to make sure the members grouped together are homogeneous with regard not only to demographic factors (age, gender etc), but also with regard to the nature of their benefit slices.  But of course by doing this, you lose the ability to produce accurate member by member values, split by benefit type, slice and decrement.  ("Decrement" here means the mode of exit, e.g. death, leaving service, retirement etc).  

Instead, the approach I prefer is to continue to produce the raw cashflows, and to keep them separately for each member, but to combine them as far as possible (again for each member) without losing the information about benefit type and nature.  This means not only that accurate values split for each member by benefit are produced, but information for accurate risk management (for stochastic modelling or for cashflow matching by nature and type) is preserved.

One example is that for a given member, benefit type, slice and decrement, cashflows at the end of year n and the start of year n+1  can be combined without loss of accuracy, because they have the exact same characteristics including the date of payment.

With this and other smart processing, the number of cashflows that need to be retained can be reduced by a factor of 100 or even more.